Basic Mathematics Solved Problems | Topics - Contents
Prime Factorization
This is a method of writing a number as a product of prime numbers.Prime Number
- A natural number greater than 1 that is not a product of two smaller natural numbers.
- A positive integer greater than 1 that can only be divided by itself and 1 without leaving a remainder.
- A prime number is a whole number greater than 1 whose only factors are 1 and itself.
- A number that cannot be divided by any other number except itself and the number.
- A prime number is a positive integer that has exactly two positive divisors, 1 and it self.
- Examples: 2, 3, 5, 7, 11, ... One (1) is not a prime number.
Composite Number
- is a natural number with more than two factors.
Suggested Solution:
- Using divisibility rules check the given number if it is divisible by prime numbers (start with the lowest) (2, 3, 5, 7, 11, 13, 17, 19, 23, ...)
- If possible divide the number by that prime number
- Repeat process to the quotient until the remaining quotient is a prime number. Note: If you're using the factor tree this solution is a good one. It is a bad idea to start a factor tree by dividing large numbers - although this is not wrong but dividing large number is quite difficult to do compared to dividing smaller numbers, but you can do it it's not a problem.
Examples
- Find the prime factors of 100.
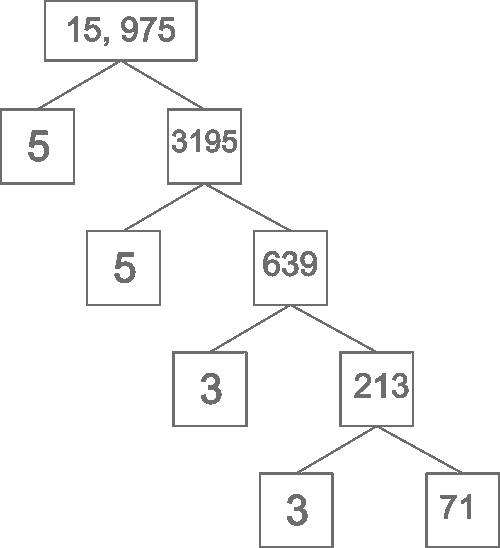
- Find the prime factors of 15, 975.
100 is divisible by 2
100 ÷ 2 = 50
50 ÷ 2 = 25
25 ÷ 5 = 5, since the last quotient is 5, a prime number stop here.
100 ÷ 2 = 50
50 ÷ 2 = 25
25 ÷ 5 = 5, since the last quotient is 5, a prime number stop here.

Thus the prime factors of 100 = 2 x 2 x 5 x 5